Cryptology is divided into cryptography — the encryption of information — and cryptanalysis, the extraction of information from already-encrypted data. This blog post only deals with the first part: encrypting information.
Cryptography — or simply “encryption” — has become indispensable on the Internet. Fortunately, most sites are now protected with HTTPS. That means the connection from your browser to the server you request is encrypted end-to-end. So nobody can tamper with that connection without it being noticeable. More on that at the end of the article.
Other areas are encrypted too, for example data stored on a remote server (keyword: cloud). With a good encryption strategy even the cloud provider cannot read your data. And WhatsApp messages now use Signal’s strong encryption, making messages unreadable to anyone who is not the intended recipient.
But let’s start from the very beginning.
What is cryptography?
Cryptography is the science of protecting information from manipulation and unauthorized reading, while ensuring who is communicating with whom.
A human-readable text (plaintext) is made unreadable to others by encryption. This process of encrypting is called enciphering. The opposite is deciphering — turning unreadable secret text (ciphertext) back into plaintext. To turn a cipher back into plaintext you need a secret, the so-called key. I’ll explain that with an example.
The simplest method is the Caesar cipher. Here every letter of the plaintext is replaced by a letter that comes later in the alphabet.
Plaintext: a b c d e f g h i j k l m n o p q r s t u v w x y z
Cipher: D E F G H I J K L M N O P Q R S T U V W X Y Z A B CAs you can see, the alphabet was simply shifted by three letters. So an A (first position in the alphabet) becomes D (fourth position in the alphabet).
If we want to encrypt the plaintext “caesar”, we replace each letter using our shifted alphabet. The “c” becomes “F”, the “a” becomes “D”, and so on. The resulting cipher is “FDHVDU”. To a person this cipher makes no sense because it isn’t a known word. But if you know how the enciphering works, you can reverse it (decipher). We can simply shift each letter in the cipher “FDHVDU” three positions back in the alphabet. Then we have the word “caesar” again.
Secrets
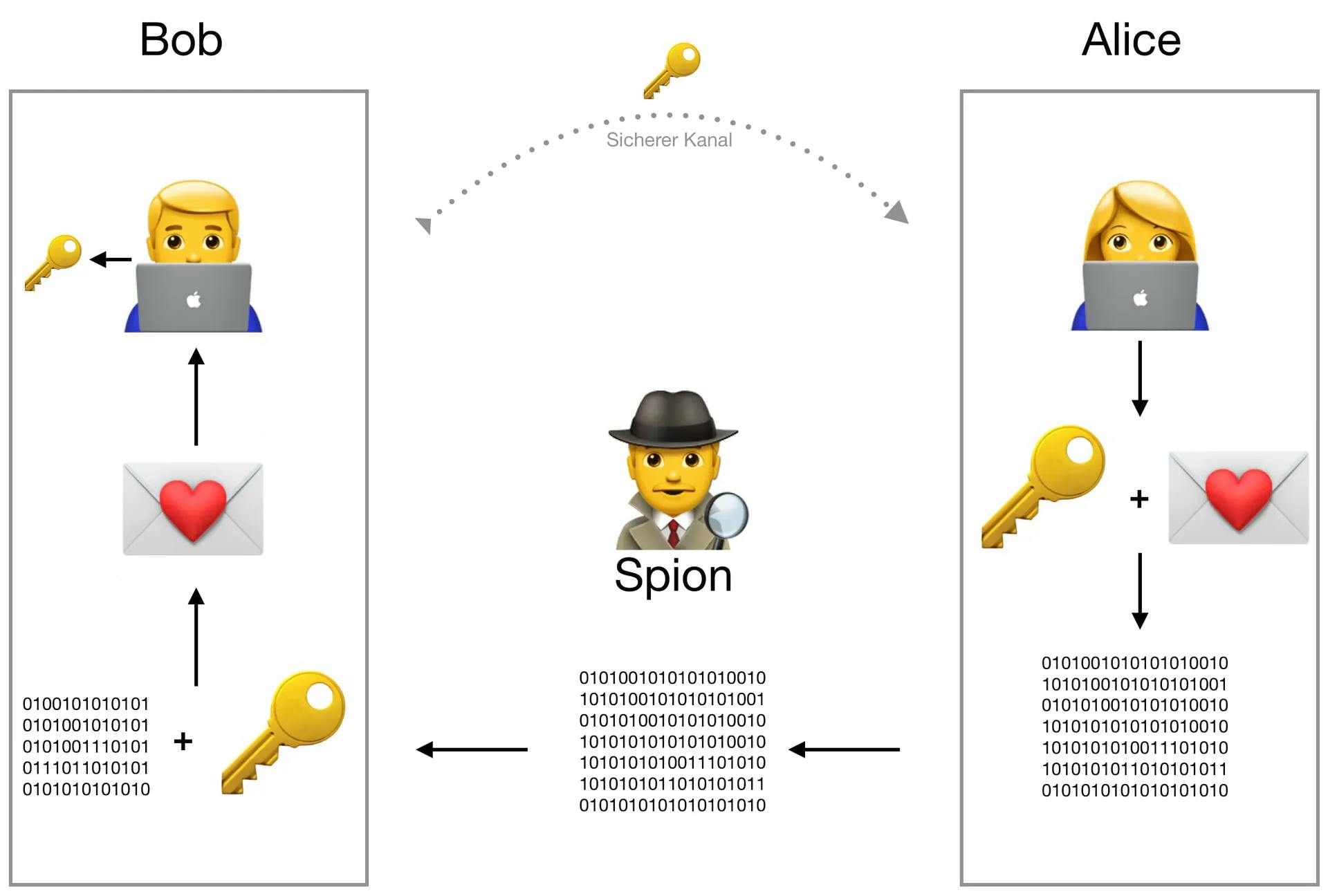
With this method you notice that Alice (the encipherer / sender) and Bob (the decipherer / receiver) must know how many positions to shift. The information “how many positions” is the secret — the key of the encryption. Since both parties must know the same secret, this is called symmetric encryption. The entire strength of an encryption lies in this key. The method can be known to everyone and yet nobody can decipher the text as long as they don’t know the key. All modern schemes build on this. Anyone can implement the encryption method — it’s standardized. The only thing that must never become known is the secret key! A modern example is AES (Advanced Encryption Standard). This algorithm is used everywhere today, as we’ll see later.
Attacks
Suppose the sender doesn’t deliver the cipher directly to the receiver, but for example the mail carrier takes it and tries to read it before delivering it — that’s called a man-in-the-middle attack.
If the method is known to a third party (e.g., the mail carrier), they still can’t do anything with the cipher “FDHVDU” because they don’t know how many positions to shift the letters. If the attacker still wants to try to decipher the text, they have no choice but to try every shift and check whether a sensible plaintext appears. This kind of attack is called brute force — simply trying all possibilities. With our alphabet this is not difficult because there are only 26 possibilities.
Modern cryptography
With the Caesar cipher we saw there are 26 possibilities to guess the secret and that both parties (sender and receiver) must know the secret. Modern methods used on the Internet use other techniques to increase the security of transmission over a single channel.
Modern secrets
Imagine that in the symmetric Caesar scheme the secret is a real physical key — like your front door key — and the method is a safe with a lock. Both parties need the same key. The sender locks the box with the key, while the receiver opens the box with a copy of the key. Somehow that key must have reached both parties via a secure route that ensured nobody — not even the mail carrier — ever saw or copied it.
On the Internet this is very difficult because we don’t have a second channel besides the Internet to send the key quickly and securely. So people invented a method where you don’t have to transmit the secret key. Instead of a shared key for both parties, the lock is replaced by a padlock. This method is called asymmetric encryption or the public‑private‑key scheme.

Imagine the receiver 👨💻 now builds a padlock 🔓 (public key) and a key 🔑 (private key) for his secret box. The key is the secret that only the receiver can use to open the padlock. This key never leaves the owner — nobody will ever see it. The padlock, however, can be seen by anyone and can be closed by anyone: you just push the shackle down and it locks. The receiver can duplicate this opened padlock many times and give it to anyone who wants to send him something secret. Or hang a few on his front door so anyone can take one. The mail carrier 🕵️♂️ cannot do anything with an open padlock.
A sender 👩💻 takes the open padlock and locks a box containing a message with it. Nobody without the matching key can ever open that padlock again. Not even the mail carrier — at best they have another open padlock but not the key. The only one with the matching key is Bob, the receiver.
Keys go digital
All protocols that protect the communication channel on the Internet are based on this paradigm. Of course computers don’t exchange physical padlocks and keys. Computers use mathematical methods to model this paradigm digitally. In the RSA scheme (named after Rivest, Shamir, and Adleman) prime numbers are multiplied, for example. RSA is therefore based on the mathematical problem of prime factorization. That means:
You pick two random prime numbers. The two primes individually form the private key.
You multiply the two prime numbers. The result is the public key.
You might think “is that it? I can just divide the public key and get the private key.” But it’s not that simple. It’s mathematically much harder to factor a number into two primes than it is to multiply two primes.
You can see this with a simple example:
Multiply in your head: 11 × 16.
Factor the number 143 into its prime factors. Hint: divide 143 by 13.
You will notice the first task is much easier than the second, even though in the second case one of the prime factors is already suggested by the hint. The same applies to computers. This is a mathematical phenomenon. In RSA much larger primes are used to make the computation harder. For more on the math behind RSA you can read Wikipedia.
There are other schemes besides RSA. Diffie–Hellman (DH) is noteworthy because it is part of current standards. It’s merely a method for exchanging a key — not an encryption method itself.
With this method both parties first generate a private key 🔑 and a public key 🔓.

They send only their public keys to the other party and keep their private keys secret. Bob’s private key 🔑👨💻 and Alice’s public key 🔓👩💻 are then combined at Bob’s side. The result is a so-called shared secret. Reversed — Alice’s private key 🔑👩💻 and Bob’s public key 🔓👨💻 — produce exactly the same secret on Alice’s side! That is the mathematical trick of the method and is based on the difficulty of the discrete logarithm problem. Exponentiation is easier to compute than its reverse, the logarithm. For an easy illustration:
the power: 10²
the logarithm: log₁₀(1000)
Again the first calculation is much simpler. For a deeper understanding of the math I also recommend Wikipedia.
Returning to the diagram: attackers can see only two public keys, from which they cannot compute the shared secret because they have not seen either party’s private key. Another trick is that both parties now use the same secret, allowing them to employ a symmetric encryption method again, which speeds up encryption/decryption. AES is usually used here.
That’s basically the current state of the art. It’s called ECDH (Elliptic Curve Diffie–Hellman). Simply put, elliptic curves extend the complexity of the logarithm problem into a multidimensional space. The result is that for the same security level computation can be much faster and key lengths much shorter. More on that later.
Modern attacks
Man-in-the-middle attacks still exist today. Unscrupulous providers sometimes try to intercept connections between you and the website you visit to insert ads or analyze whether you are downloading legal or illegal files. Intelligence agencies (for example Germany’s Bundesnachrichtendienst) are also allowed to intervene in these connections and monitor your communications. However, the encryption of websites (the “https” in your browser’s address bar) is so strong that nobody has yet succeeded in breaking the current methods. If you hear in the news that a current encryption technique is vulnerable, it usually means the software implementation has bugs; the mathematical algorithm itself remains extremely secure. The only remaining way for attackers to break encryption is brute force, trying all possible keys. But we’re no longer talking about 26 possibilities like the Caesar method. Depending on key length, even for relatively small keys there can be on the order of 900,000,000,000,000,000,000,000,000,000 possible keys.
Key length
The longer a key is in cryptography, the more different keys there can be and the harder it is to find the right one by random guessing.
Example: suppose our key may only consist of numbers and a digit may be at most 3. Then there are exactly 4 possible keys:
a) 0
b) 1
c) 2
d) 3
In computer science we think in binary rather than the familiar decimal system. So there aren’t digits 0–9 (decimal) but only 0 and 1. With those two digits we can represent a lot. If we map our four possible keys to binary, it looks like this:
Decimal₁₀ - Binary₂
a) 0₁₀ - 00₂
b) 1₁₀ - 01₂
c) 2₁₀ - 10₂
d) 3₁₀ - 11₂
I’ve appended the numeral base under the numbers so you can see at a glance which system we’re in. It may seem strange to people who’ve never thought in binary. Note that every combination of 0₂ and 1₂ occurs only once — that’s crucial. To represent decimal 0₁₀ through 3₁₀ you need two binary digits. Therefore we speak of 2 bits of information (entropy). In summary, 2 bits yield exactly four possible keys.
If we increase the bits by one to 3 bits, the number of possibilities doubles to eight. With each additional bit we again double the number of possibilities. That’s an exponential function, which means with 20 bits you already have over a million possibilities, with 30 bits a billion. At 100 bits there are already over 1 quintillion possibilities (i.e., 1,000,000,000,000,000,000,000,000,000,000 — a 1 followed by 30 zeros).
For RSA we are nowadays at a key length of 4096 bits. The number of possible keys is then no longer expressible in a way the human brain can meaningfully grasp. Interestingly, ECDH currently uses only 256-bit keys to achieve the same security level as RSA with a 4096-bit key. That’s because for RSA various shortcut mathematical tricks to compute the private key from the public key have been discovered; such tricks don’t exist for ECDH (or haven’t been found yet). Also, the logarithm problem in a multidimensional space is harder to solve than prime factorization. Thus a smaller key suffices for the same security — where “security” here means how long an attacker would need to find the private key.
Security
Key length is not the only factor for the security of an encryption method. With RSA we’ve seen that a very long key (4096 bits) can be as secure as a 256-bit ECDH key.
This is partly because different algorithms have different computational difficulty for a computer, and partly because mathematicians have found ways to shortcut the computation of private keys. The symmetric cipher Data Encryption Standard (DES) has been considered broken since 1994. Its short effective key length of only 56 bits makes it vulnerable to brute force. Also, the key schedule (generation of 16 round keys from the original key) is weak: in DES those derived keys are almost identical and thus provide an additional attack surface because they can be predicted mathematically.
A short outlook — quantum computers
Yes — they do exist in concept, but if they become practical they will break known asymmetric schemes in a thousandth of the time of a classical computer. Quantum computers have the property that a quantum bit can represent not only 0 or 1 but both states simultaneously. A quantum computer can thus consider all possibilities for reversing a public key to a private key at once. For symmetric schemes a quantum computer doesn’t have this same shortcut — it still basically has to guess the key. It can’t reverse symmetric encryption.
We desperately need asymmetric schemes on the Internet. Without them no security can be guaranteed. When you visit a website you and the server need a shared secret. But that secret can only be established over the same channel — the Internet — that carries the content. If an attacker intercepts that channel, they get both the shared secret and the encrypted content at the same time, which must be prevented. That’s why asymmetric schemes are so important: only the public key is exchanged.
The solution to the quantum-computer problem is new algorithms that do not rely on prime factorization or discrete logarithms. They are based on different mathematical problems for which quantum computers are no faster than classical ones. Research is ongoing, but so far no single scheme has yet become the standard. One reason is that it’s difficult to verify whether a new scheme is really resistant to quantum attacks since a truly capable quantum computer does not yet exist with which this can be fully tested.
Signatures
So far we’ve secured the content of a communication. An attacker cannot see what two parties are exchanging. How can I ensure that the person I’m writing to is not pretending to be someone else?
The attack
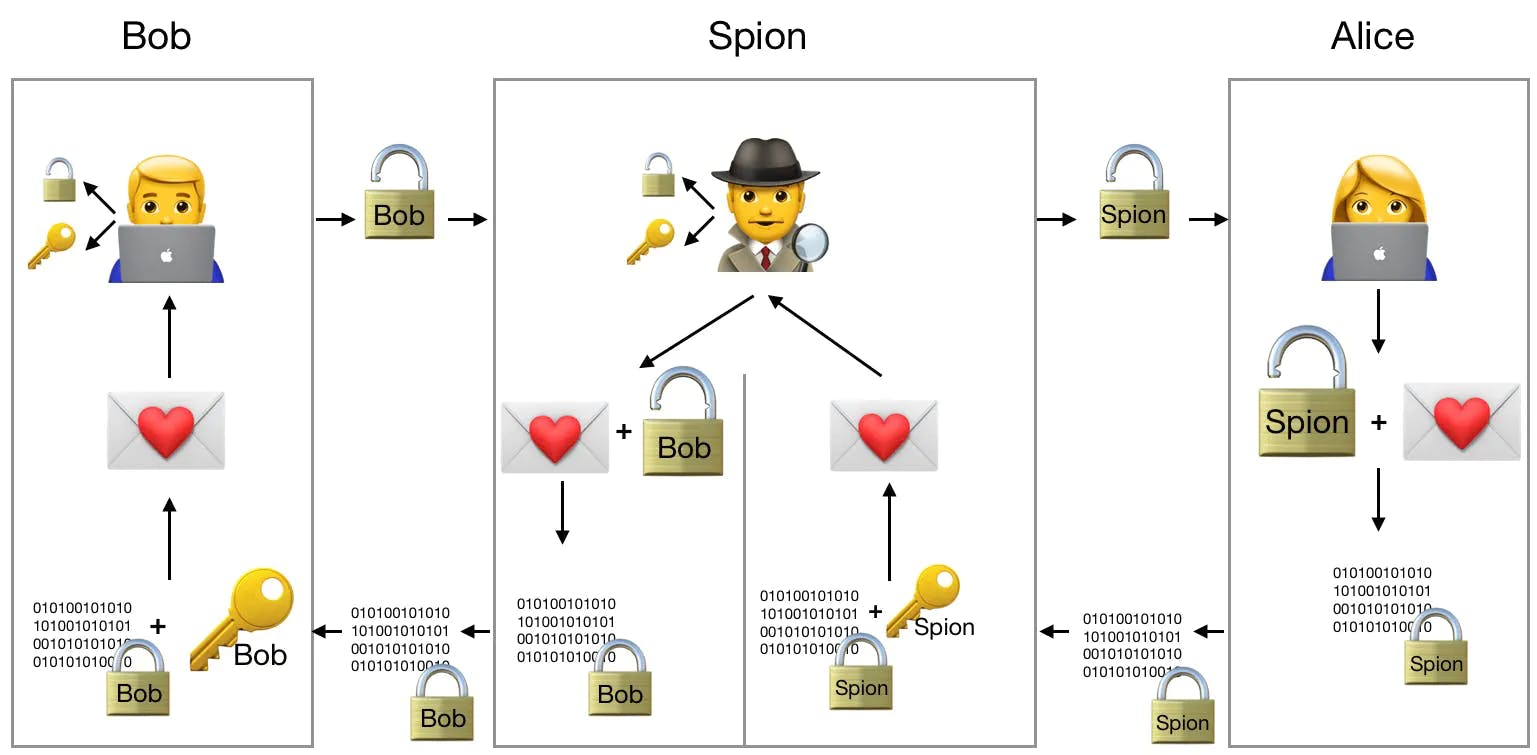
Bob now wants to send a message to Alice. Spies in the middle pretend to Bob that they are Alice, and pretend to Alice that they are Bob. That’s the classic man-in-the-middle attack against the authenticity of a person. The spies take Bob’s public key, replace it with their own, and forward it to Alice. Alice thinks the public key is Bob’s and encrypts her message to the supposed Bob. Alice sends the cipher back to the supposed Bob — which is actually the spies. The spies decrypt the message with their own private key, whose counterpart they had earlier sent to Alice. The spies can now read the message. To avoid detection they re-encrypt the message, this time with Bob’s public key, and forward it to Bob claiming it came from Alice.
Bob and Alice both think they communicated directly and securely. In reality the spies read everything.
On the Internet such spies can be anywhere — in your home router or at a major network node before the transcontinental fiber links.
The solution
Authenticity — proving the identity of a person — is achieved with signatures.
Hash
First, a hash is computed from a message. A hash can be thought of as a checksum of a text.
Example checksum:
INPUT (plaintext): caesar
Position in alphabet: 3 1 5 19 1 18
Checksum calculation: 3 + 1 + 5 + 1 + 9 + 1 + 1 + 8
OUTPUT (hash value): 29A hash function is much more complicated than a simple checksum, but similar in principle.
Important properties:
If you input the same plaintext you always get the same hash value.
If you change even one character in the plaintext, the hash value changes completely.
You can never recover the plaintext from the hash. Hash functions are cryptographic one-way streets.
Different plaintexts should never yield the same hash (avoid collisions).
You can test these four rules with current hash functions (for example using online hash generators).
With these rules we can confirm that a message has not been altered. Here’s how: the sender computes the hash of the message she composed. The receiver computes the hash of the message he received. If the two hashes differ, the message was tampered with. If they are identical, the message is unchanged.
A hash function is considered broken if a second text can be found that has the same hash value as another text. Then the original message can be replaced without changing the hash value, and the receiver will think the message was not altered.
For example, SHA‑1 (Secure Hash Algorithm 1) has been considered broken since 2005 and should no longer be used. Its successor is SHA‑2 (also known as SHA‑224, SHA‑256, SHA‑384, SHA‑512), which is currently the defined standard. The main difference is greater bit length, making collisions less likely and harder to compute. A completely different hash construction is SHA‑3, which is not yet widely used in practice.
Signing
Once the hash of a message is computed, that hash is signed. This prevents the hash itself from being manipulated and simultaneously proves who authored the message.
This works almost the same way as RSA encryption, with one crucial difference. The SENDER now creates a public key and a private key. The sender then encrypts the hash of her message with her own public key. The message together with the encrypted hash (the signature) is sent to the receiver. And here comes the big difference to RSA encryption: the sender publishes her private key!
Like a phonebook anyone can look up which key belongs to the sender. The receiver can then decrypt the signature with the sender’s public key. The visible hash extracted from the signature can then be compared with the hash the receiver computed locally. If they match, the message clearly came from the expected sender and has not been altered.
It is important to understand that the message itself does not have to be encrypted for this to work. A publicly visible message can be signed so that its author is clearly identified. This is important, for example, in digital contracts so that no party can later deny their signature.
Key management
Whether signing or asymmetric encryption — the keys themselves must be securely delivered to the people who need them. You can imagine key management as a big phonebook. In that phonebook are people’s names and next to them the public key for, e.g., RSA encryption and also the private key for that person’s signatures. (The two keys must always be generated separately and must never be related.)
If you want to verify someone’s signature you can just look it up in that phonebook. The same applies when composing messages and encrypting them with the recipient’s public key.
The problem with this phonebook is trust. If the phonebook is operated centrally you must trust the organization that provides it. If the organization is corrupt or has malicious intent, a key can simply be swapped and a man-in-the-middle attack carried out.
That’s why in cryptology everything depends on trust — and distrust.
Everyday examples
Secure websites — https
Here we have decentralized key management. The Internet community has agreed to trust certain certificate authorities (CAs). These are allowed to issue certificates for websites. The websites in turn sign the keys for their HTTPS connections with these certificates.
When you open https://farbenmeer.de, our server sends you a public key that you should use to encrypt any data before sending it back to the server. That public key is signed with a key/certificate from a certificate authority. Since your browser trusts that CA, it also trusts that the public key actually belongs to the farbenmeer site and hasn’t been swapped out by someone else.
If a CA becomes corrupt, it can issue certificates for farbenmeer.de to people who don’t own the site. They can then pretend to be farbenmeer.de and deliver malicious content such as viruses or trojans.
A certificate authority therefore must follow strict rules to be trusted. If it doesn’t, trust can be revoked and all websites with certificates from that CA will be considered insecure by browsers and become inaccessible.
WhatsApp uses end‑to‑end encryption with centralized key management. That means messages are encrypted from sender to receiver. Nobody — not even WhatsApp itself — can read the content. An attacker therefore has to compromise the end device to learn the message contents. That’s why Germany has the legal option of a state trojan: a trojan installed by a law enforcement agency on the end device to capture data (e.g., chat contents). That’s just a side note.
Key management for WhatsApp runs centrally through WhatsApp/Facebook’s servers. The phonebook mentioned above is therefore centrally located. Only Facebook can make changes. If Facebook wanted to manipulate a key, or was compelled by law to do so, it might go unnoticed and a man-in-the-middle attack could be performed easily.
If you go into a WhatsApp chat’s settings you’ll see “Encryption.” Tap that. You’ll then see a QR code and the fingerprint of the shared secret derived from the other person’s public key. You can compare that code to make sure WhatsApp hasn’t tampered with your keys.
