Die Kryp­to­logie unterteilt sich in die Kryp­to­grafie, also das Verschlüsseln von Informationen, und die Kryptoanalyse, das Extrahieren von Informationen aus bereits verschlüsselten Daten. Dieser Blogpost befasst sich nur mit dem ersten Teil, dem Verschlüsseln von Informationen.

Kryp­to­grafie - oder auch einfach "Verschlüsselung" - ist im Internet unabdingbar geworden. Inzwischen sind - zum Glück - die meisten Seiten mit https geschützt. Das heißt die Verbindung von deinem Browser zu dem Server, den du anfragst, ist durchgehend verschlüsselt. Also kann niemand diese Verbindung manipulieren, ohne dass dies auffallen würde. Am Ende des Artikels mehr dazu.
Auch andere Bereiche sind verschlüsselt, wie z.B. Daten, die auf einem fremden Server (Stichwort Cloud) liegen. So kann bei einer guten Verschlüsselungsstrategie selbst der Cloudbetreiber deine Daten nicht einsehen. Und auch die Nachrichten in WhatsApp haben inzwischen die starke Verschlüsselung von Signal eingebaut und so die Nachrichten unkenntlich gemacht, für alle die nicht Empfänger oder Empfängerin der Nachricht sind.

Aber nun mal von ganz vorne.

Was ist Kryp­to­grafie?

Kryp­to­grafie ist die Wissenschaft, Informationen vor Manipulation und unerlaubtem Lesen zu schützen und dabei sicherzustellen wer mit wem kommuniziert.

Ein menschenlesbarer Text (Klartext / plain text) wird durch eine Verschlüsselung für Andere unlesbar gemacht. Diesen Prozess des Verschlüsselns nennt man Chiffrierung. Das Gegenteil wäre dann die Dechiffrierung, also aus unlesbarem Geheimtext (Chiffre) wieder einen Klartext zu erzeugen. Um eine Chiffre wieder in Klartext zu verwandeln benötigt man ein Geheimnis, den sogenannten Key. Ich erkläre das gleich an einem Beispiel.

Die einfachste Methode ist die Caesar-Verschlüsselung. Hier wird jeder Buchstabe des Klartextes durch einen Buchstaben ersetzt, der später im Alphabet kommt.

Klartext:  a b c d e f g h i j k l m n o p q r s t u v w x y z
Chiffre:   D E F G H I J K L M N O P Q R S T U V W X Y Z A B C

Wie dir auffällt wurde das Alphabet einfach um drei Buchstaben verschoben. So wird aus einem A (erste Position im Alphabet) ein D (vierte Position im Alphabet).
Wollen wir nun den Klartext "caesar" verschlüsseln, so ersetzen wir jeden Buchstaben durch unser neues Alphabet. Aus dem "c" wird ein "F", aus dem "a" ein "D" und so weiter. Daraus ergibt sich am Ende die Chiffre "FDHVDU". Für einen Menschen macht diese Chiffre keinen Sinn mehr, da es kein bekanntes Wort ist. Weiß man jedoch wie das Verfahren der Chiffrierung funktioniert, dann kann man es auch wieder rückgängig machen (Dechiffrieren). Wir können nun einfach für jeden Buchstaben in der Chiffre "FDHVDU" drei Positionen im Alphabet zurück gehen. Und schon haben wir wieder das Wort "caesar".

Geheimnisse

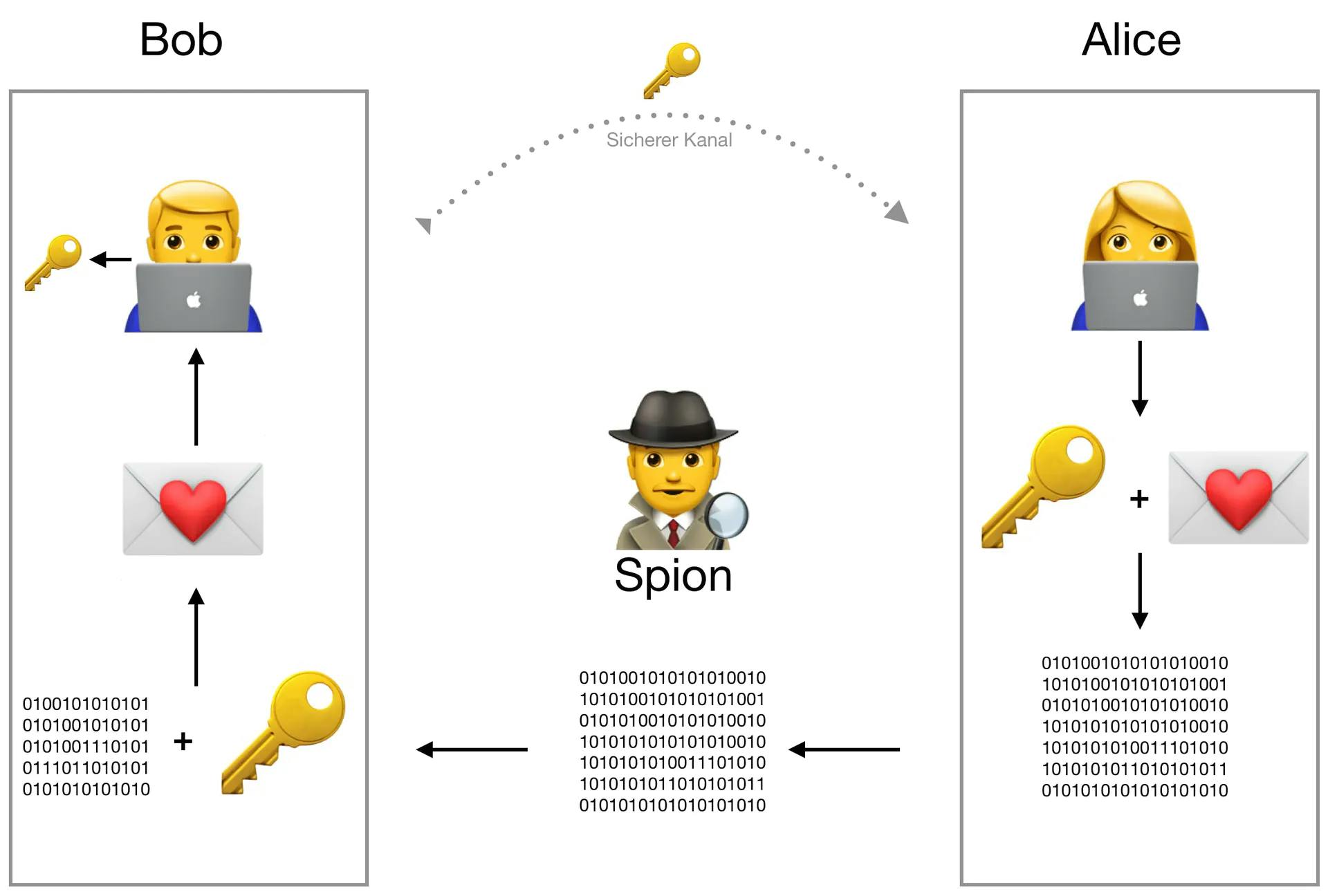
Bei dieser Methode fällt auf, dass Alice, die Chiffrierende (Senderin) und Bob, der Dechiffrierende (Empfänger) wissen müssen um wie viele Positionen sie verschieben müssen. Die Information "Wie viele Positionen" ist das Geheimnis, der Schlüssel (Key) der Verschlüsselung also. Und da beide Parteien das gleiche Geheimnis wissen müssen, nennt man dies symmetrische Verschlüsselung. Die ganze Stärke einer Verschlüsselung liegt in diesem Schlüssel. Das Verfahren kann jedem bekannt sein und trotzdem kann niemand den Text dechiffrieren, so lange man den Schlüssel nicht kennt. Alle modernen Verfahren bauen hierauf auf. Jeder kann das Verschlüsselungsverfahren nachbauen, es ist standardisiert. Das Einzige was niemals bekannt werden darf, ist der geheime Schlüssel! Ein modernes Beispiel ist der AES (Advanced Encryption Standard). Dieses Verfahren kommt heutzutage überall zum Einsatz, wie wir später sehen werden.

Angriffe

Nehmen wir an, der Sender bringt die Chiffre nicht direkt zum Sender, sondern z.B. der Postbote nimmt sie entgegen und versucht sie zu lesen bevor er sie dem Empfänger weiter gibt, so nennt man dies einen Man-in-the-Middle-Angriff.

Ist das Verfahren nun einem Dritten (z.B. dem Postboten) bekannt, so kann er trotzdem nichts mit der Chiffre "FDHVDU" anfangen, da er nicht weiß um wie viele Stellen er die Buchstaben verschieben muss. Will der Angreifer trotzdem versuchen die Chiffre zu Dechiffrieren, so bleibt ihm nichts anderes übrig, als jede Positionsverschiebung auszuprobieren und zu prüfen ob ein sinnvoller Klartext entsteht. Diese Art des Angriffs nennt man brute force, also einfach alle Möglichkeiten ausprobieren. Bei unserem Alphabet ist dies keine schwierige Aufgabe, da es nur 26 Möglichkeiten gibt.

Moderne Kryp­to­grafie

Bei der Caesar-Verschlüsselung haben wir festgestellt, dass es 26 Möglichkeiten gibt um das Geheimnis zu erraten und dass beide Parteien (Senderin und Empfänger) das Geheimnis kennen müssen. Moderne Verfahren, wie sie im Internet zum Einsatz kommen, benutzen andere Methoden, um die Sicherheit der Übertragung über einen einzigen Kanal zu erhöhen.

Moderne Geheimnisse

Stell dir vor bei der symmetrischen Verschlüsselung aus der Caesar-Methode ist das Geheimnis ein echter physikalischer Schlüssel – wie von deiner Haustür – und das Verfahren ein Safe mit einem Schloss. Beide Parteien benötigen den gleichen Schlüssel. Der Sender schließt die Box mit dem Schlüssel ab, während der Empfänger die Box mit einer Kopie des Schlüssels wieder aufschließt.
Irgendwie muss dieser Schlüssel also an beide Parteien gelangt sein, auf einem sicheren Weg, bei dem sichergestellt werden konnte, dass niemand – auch kein Postbote – diesen Schlüssel je gesehen hat und kopieren konnte.

Im Internet ist dies sehr schwer, da wir keinen zweiten Kanal neben dem Internet haben um den Schlüssel schnell genug und sicher zu versenden. Daher hat man sich eine Methode einfallen lassen, bei der man den geheimen Schlüssel nicht übertragen muss. Anstelle eines gemeinsamen Schlüssels für beide, hat man das Schloss nun durch ein Vorhängeschloss ersetzt. Dieses Verfahren nennt man asymmetrische Verschlüsselung oder auch Public-Private-Key-Verfahren.

Stell dir vor, der Empfänger 👨‍💻 baut nun ein Vorhängeschloss 🔓 (public-key) und einen Schlüssel 🔑 (private-key) für seine geheime Box. Der Schlüssel ist das Geheimnis, mit dem nur der Empfänger das Vorhängeschloss öffnen kann. Dieser Schlüssel verlässt niemals den Eigentümer, niemand wird ihn jemals sehen. Das Vorhängeschloss kann jedoch jede Person sehen und von jeder Person geschlossen werden, denn man muss das Schloss dafür nur fest zusammendrücken und schon ist es verschlossen. Der Empfänger kann dieses geöffnete Vorhängeschloss nun vielfach duplizieren und an jede Person herausgeben, die ihm etwas geheimes mitteilen möchte. Oder hängt gleich ein Paar davon vor seine Haustüre, so kann jeder einfach eins mitnehmen. Der Postbote 🕵️‍♂️ kann mit dem geöffneten Vorhängeschloss nichts anfangen.
Eine Senderin 👩‍💻 nimmt nun das offene Vorhängeschloss und verschließt damit eine Box, die eine Nachricht enthält. Niemand ohne den passenden Schlüssel kann nun das Vorhängeschloss der Box jemals wieder öffnen. Auch nicht der Postbote, der hat im Zweifel nur ein weiteres geöffnetes Vorhängeschloss aber nicht den Schlüssel. Der Einzige mit dem passenden Schlüssel ist Bob, der Empfänger.

Schlüssel werden digital

Alle Verfahren, die den Kommunikationskanal im Internet schützen, basieren auf diesem Paradigma. Natürlich werden bei Computern keine Vorhängeschlösser und Schlüssel ausgetauscht. Computer nutzen mathematische Verfahren um dieses Paradigma digital abzubilden. Bei dem RSA Verfahren (benannt nach Rivest, Shamir und Adleman) werden z.B. Primzahlen multipliziert.
RSA basiert also auf dem mathematischen Problem der Primfaktorzerlegung. Das heißt:

1. Man wählt zwei zufällige Primzahlen. Beide Primzahlen einzeln sind der private key.
2. Man multipliziert die beiden Primzahlen. Das Ergebnis ist nun der public key.

Nun denkst du dir sicher "und das wars? Ich kann doch einfach den public key auseinander dividieren und schon habe ich den private key." So einfach ist das aber nicht. Es ist mathematisch viel schwieriger eine Zahl in zwei Primzahlen zu zerlegen, als zwei Primzahlen zu multiplizieren.

Das kann man auch an einem einfachen Beispiel sehen:

1. Multipliziere folgendes im Kopf: 11 x 16.
2. Zerlege die Zahl 143 in ihre Primzahlen. Tipp: Teile die Zahl 143 durch 13.

Du wirst gemerkt haben, dass dir die erste Aufgabe wesentlich einfacher von der Hand ging als die zweite, obwohl dir hier schon eine der beiden Primzahlen bekannt war. Genauso geht es Computern auch. Denn dies ist ein mathematisches Phänomen. Beim RSA Verfahren werden natürlich viel größere Primzahlen verwendet, um die Berechnung zu erschweren.
Mehr zum mathematischen Teil von RSA kannst du bei Wikipedia nachlesen.

Es gibt auch noch andere Verfahren als RSA. Der Diffie-Hellman Schlüsselaustausch (DH) ist hier nennenswert, da er ein Teil des aktuellen Standards ist. Es handelt sich hierbei lediglich um ein Verfahren zum Austausch eines Schlüssels! Nicht um ein Verfahren zum Verschlüsseln selbst!

Bei dieser Methode generieren beide Parteien zuerst einen private key 🔑 und einen public key 🔓.

Sie senden aber nur jeweils ihren eigenen public key an die andere Partei und behalten ihren eigenen private key unter Verschluss. Der private key von Bob 🔑👨‍💻 und der public key von Alice 🔓👩‍💻 werden nun bei Bob zusammengerechnet. Daraus ergibt sich ein sogenanntes shared secret. Denn umgedreht, also der private key von Alice 🔑👩‍💻 und der public key von Bob 🔓👨‍💻, ergeben zusammen das exakt selbe Geheimnis auf Alice Seite! Dies ist der mathematische Trick des Verfahrens und basiert auf der Problematik des diskreten Logarithmus. Das heißt, dass Potenzierung einfacher zu berechnen ist, als der Logarithmus. Auch hier der Beweis zum selber rechnen:

1. die Potenz: 10²
2. den Logarithmus: log₁₀(1000)

Auch hier fällt auf, dass die erste Rechnung viel einfacher zu lösen ist. Für ein tieferes Verständnis der Mathematik empfehle ich auch hier Wikipedia.

Zurück zur Abbildung, können Angreifende demnach nichts sehen außer zwei public keys, aus denen man aber nicht das shared secret errechnen kann, da man keinen private key der beiden Parteien gesehen hat.
Ein weiterer Trick ist, dass nun beide Parteien das gleiche Geheimnis verwenden und somit wieder ein symmetrisches Verschlüsselungsverfahren verwendet werden kann, was die Geschwindigkeit der Dechiffrierung erhöht. Hier kommt dann meist der AES zum Einsatz.

Und damit ist dann auch schon fast der aktuelle Stand der Technik erklärt. Dieser heißt ECDH (Elliptic curve Diffie-Hellman). Hier wird vereinfacht gesagt die Komplexität des Logarithmus auf einen mehrdimensionalen Raum ausgeweitet. Das hat zur Folge, dass bei gleichbleibender Sicherheit die Berechnungsgeschwindigkeit enorm erhöht werden kann und die Schlüssellänge dabei viel kürzer werden kann. Hierzu später mehr.

Moderne Angriffe

Auch heute gibt es noch man-in-the-middle Angriffe. So versuchen z.B. unseriöse Anbieter im Internet die Verbindungen zwischen dir und deiner aufgerufenen Webseite abzufangen und dort z.B. Werbung zu platzieren oder zu analysieren ob du gerade legale oder doch illegale Dateien herunterlädst. Auch der Bundesnachrichtendienst darf in diese Verbindung eingreifen und deine Kommunikation überwachen. Allerdings ist die Verschlüsselung der Webseiten (Sichtwort "https" in der Adressleiste des Browsers) so stark, dass es noch niemand geschafft hat, die aktuellen Methoden zu brechen. Wenn du in den Nachrichten hörst, dass eine aktuelle Verschlüsselungstechnik angreifbar ist, dann liegt das meist daran, dass die Umsetzung der Technik innerhalb der Software Fehler hat; das mathematische Verfahren ist aber bis heute extrem sicher. Die einzige Möglichkeit für Angreifende die Verschlüsselung zu knacken bleibt demnach der brute force Angriff, bei dem man alle möglichen Schlüssel ausprobiert. Allerdings reden wir hier nicht mehr von 26 Möglichkeiten wie zu Beginn bei der Caesar-Methode. Je nach Länge des verwendeten Schlüssels ergeben sich hier selbst bei sehr kleinen Schlüsseln über 900.000.000.000.000.000.000.000.000 Möglichkeiten.

Schlüssellänge

Je länger ein Schlüssel in der Kryptographie ist, desto mehr verschiedene Schlüssel kann es geben und desto schwieriger ist es diesen durch zufälliges Ausprobieren zu finden.

Schauen wir uns ein Beispiel an: Sagen wir, unser Schlüssel darf nur aus Zahlen bestehen und eine Zahl darf maximal die Zahl 3 sein. Dann gibt es genau 4 mögliche Schlüssel, nämlich:

a) 0
b) 1
c) 2
d) 3

In der Informatik denken wir im Binärsystem und nicht im uns allen bekannten Dezimalsystem. Demnach gibt es nicht die Zahlen 0 bis 9 (Dezimal), sondern nur die Zahlen 0 und 1. Mit diesen zwei Zahlen kann man jedoch sehr viel abbilden. Wollen wir unsere 4 möglichen Schlüssel nun binär abbilden, so würde das so aussehen:

Dezimal₁₀ - Binär₂
a) 0₁₀ - 00₂
b) 1₁₀ - 01₂
c) 2₁₀ - 10₂
d) 3₁₀ - 11₂

Unten an den Zahlen habe ich das Zahlensystem angehängt, damit du schneller siehst in welchem System wir uns gerade befinden. Sieht nun erst einmal komisch aus für Menschen, die noch nie im Binärsystem gedacht haben. Achte darauf, dass jede Kombination aus 0₂ und 1₂ nur einmal vorkommt. Dies ist entscheidend. Um die Zahlen 0₁₀ bis 3₁₀ abzubilden, benötigen wir im binären System zwei Ziffern. Daher spricht man hier von 2 Bit Informationsgehalt (Entropie).
Zusammengefasst heißt das, dass 2 Bit eine Möglichkeit von genau vier Schlüsseln liefert.

Erhöhen wir die Bits um eine Ziffer, also auf 3 Bit, verdoppelt sich die Anzahl der Möglichkeiten auf acht. Da wir jede Möglichkeit von a) bis d) nun zweimal haben. Einmal mit einer 0₂ und einmal mit einer 1₂ vorangestellt.

Bei jedem weiteren Bit verdoppeln wir wieder die Anzahl der Möglichkeiten. Das ist eine exponentielle Funktion und hat zur Folge, dass wir mit 20 Bit schon bei über einer Millionen, mit 30 Bit schon bei einer Milliarde Möglichkeiten sind. Bei 100 Bit gibt es dann schon über 1 Quintillionen, also 1.000.000.000.000.000.000.000.000.000.000 Möglichkeiten verschiedener Schlüssel, also eine Eins gefolgt von 30 Nullen.

Bei RSA sind wir heutzutage bei einer Schlüssellänge von 4096 Bit angekommen. Die Anzahl der möglichen Schlüssel ist somit nicht mehr in einer Zahl auszudrücken, die das menschliche Gehirn noch begreifen kann.
Interessant ist, dass z.B. beim ECDH aktuell nur 256 Bit als Schlüssellänge verwendet werden, bei der gleichen Sicherheit von RSA mit 4096 Bit Schlüssellänge. Dies liegt daran, dass beim RSA Verfahren schon diverse "Abkürzungen" – also mathematische Tricks – zum Berechnen des private keys, aus dem public key heraus, gefunden wurden, die es bei ECDH nicht gibt, bzw. die noch von keinem Menschen oder keiner Maschine entdeckt wurden. Außerdem ist das Problem des Logarithmus im mehrdimensionalen Raum aufwendiger zu lösen als das Problem der Primfaktorzerlegung. Somit genügt ein kleinerer Schlüssel bei gleicher Sicherheit. Wobei Sicherheit in diesem Kontext bedeutet, wie viel Zeit ein Angreifer braucht, um den privaten Schlüssel herauszufinden.

Sicherheit

Für die Sicherheit einer Verschlüsselungsmethode ist nicht nur die Länge des Schlüssels wichtig. Bei RSA haben wir gesehen, dass wir einen sehr langen Schlüssel (4096 Bit) verwenden und dieser genauso sicher ist wie ein 256 Bit ECDH Schlüssel.

Das liegt einerseits daran, dass die Verfahren für einen Computer unterschiedlich schwer zu berechnen sind, andererseits dass Mathematikerinnen und Mathematiker Wege gefunden haben, um die Berechnung eines Schlüssels abzukürzen. Das symmetrische Verschlüsselungsverfahren Data Encryption Standard (DES) gilt z.B. schon seit 1994 als geknackt. Seine kurze Schlüssellänge von effektiv nur 56 Bit macht ihn durch brute force angreifbar.
Außerdem gilt die Schlüsselpermutation als sehr schwach. Dabei werden aus dem eigentlichen Schlüssel 16 weitere Schlüssel erzeugt. Bei DES sind diese jedoch fast identisch und bieten somit eine weitere Angriffsfläche, da sie mathematisch vorhergesagt werden können.

Kleiner Ausblick – Quantencomputer

Richtig gehört. Es gibt sie zwar noch nicht wirklich aber wenn sie kommen werden sie die bekannten asymmetrischen Verfahren brechen, in einem Tausendstel der Zeit eines klassischen Computers. Quantencomputer haben die Eigenschaft, dass sie nicht nur binär den Zustand 0 und 1 in einem Bit darstellen können, sondern sie können beide Zustände zur gleichen Zeit haben. Ein Quantenkomputer kann so alle Möglichkeiten der Rückwärtsberechnung von einem public key auf einen private key gleichzeitig in Betracht ziehen und damit rechnen.
Für die symmetrischen Verfahren hat ein Quantencomputer diese "Abkürzung" nicht wirklich parat, da er hier ebenfalls nur raten kann was der Schlüssel war. Er kann hier nichts zurückberechnen.
Allerdings brauchen wir asymmetrische Verfahren im Internet sehr dringend. Ohne sie kann keine Sicherheit garantiert werden. Denn wenn du eine Webseite aufrufst, dann benötigen du und der Server der aufgerufenen Seite ein geteiltes Geheimnis. Dieses Geheimnis kann aber nur über den selben Kanal – das Internet – wie der Content selbst geliefert werden. Schneidet ein Angreifer diesen Kanal mit, so hat er das geteilte Geheimnis UND den verschlüsselten Content gleichzeitig, was ja unbedingt verhindert werden soll. Deshalb sind asymmetrische Verfahren so wichtig. Denn bei asymmetrischen Verfahren wird nur der public key ausgetauscht.

Die Lösung des Quantencomputer-Problems sind neue Verfahren, die nicht auf der Problematik der Primfaktorzerlegung oder des Logarithmus setzen. Es wird auf ein anderes mathematisches Problem gesetzt, bei dem Quantencomputer genauso langsam sind wie klassische Computer. Hier wird derzeit noch fleißig geforscht. Es hat sich jedoch bisher noch kein Verfahren durchgesetzt um standardisiert zu werden. Das liegt vor allem daran, dass nicht überprüft werden kann, ob das neue Verfahren wirklich resistent gegen einen Quantencomputer ist, da ein echter Quantencomputer noch nicht existiert, mit welchem man dies real testen könnte.

Signaturen

Bisher haben wir den Inhalt einer Kommunikation gesichert. Ein Angreifer kann also nicht sehen was zwei Parteien miteinander kommunizieren. Wie kann ich jedoch sicherstellen, dass die angeschriebene Person sich nicht für jemanden Anderen ausgibt?

Der Angriff

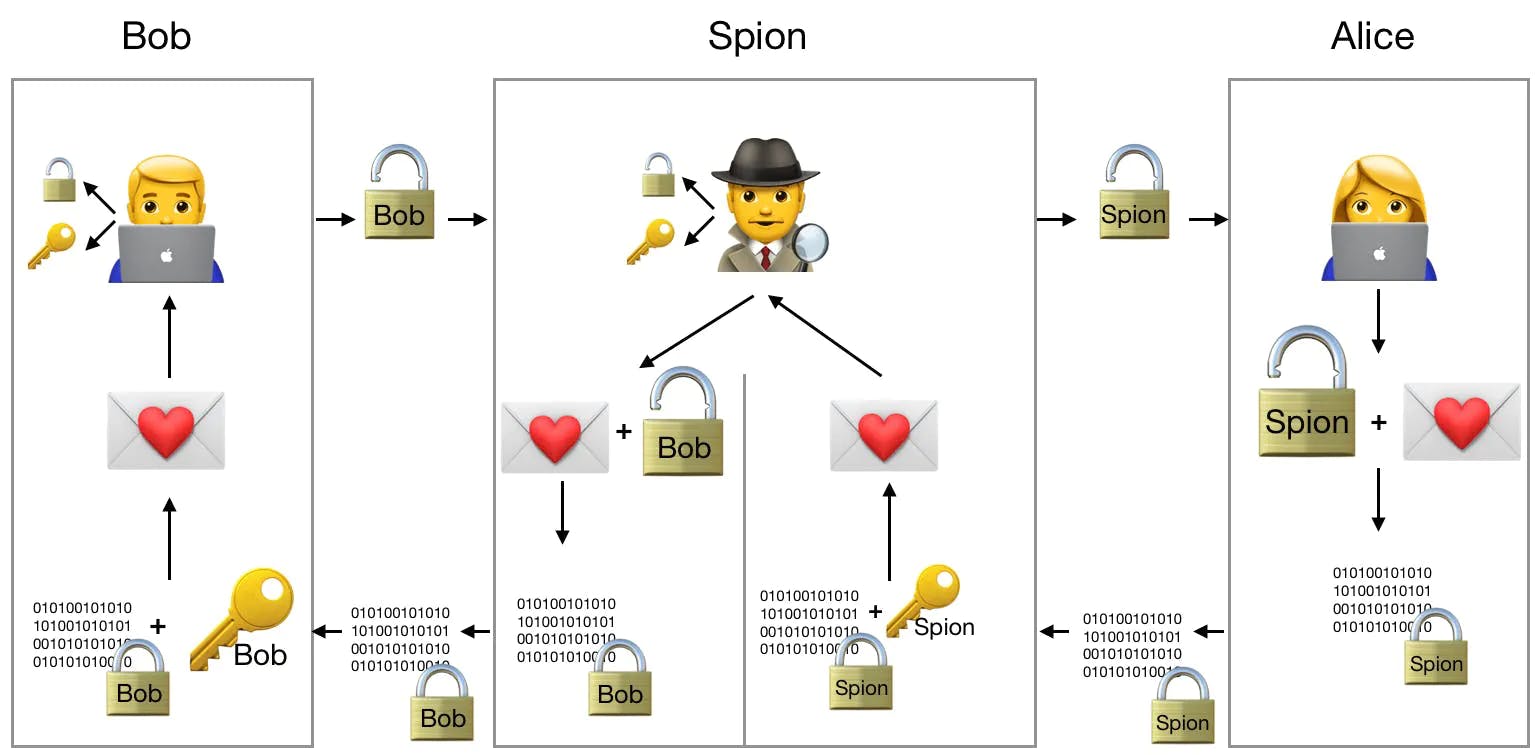
Bob will nun eine Nachricht an Alice senden. Die Spionierenden in der Mitte geben sich gegenüber Bob als Alice aus und gegenüber Alice als Bob. Das ist der klassische man-in-the-middle Angriff auf die Authentizität einer Person. Die Spionierenden nehmen also den public key von Bob entgegen, ersetzen diesen durch den Eigenen und senden ihn an Alice weiter. Alice denkt, der public key kommt von Bob und verschlüsselt damit ihre Nachricht an den vermeintlichen Bob. Alice sendet die Chiffre an den vermeintlichen Bob zurück, was in Wirklichkeit aber die Spionierenden sind. Diese entschlüsseln die Nachricht mit dem eigenen private Key, dessen Gegenstück sie vorhin an Alice gesendet haben. Die Spionierenden können nun die Nachricht lesen. Damit es nicht auffällt verschlüsseln sie die Nachricht wieder. Diesmal mit Bob's public key und senden die Nachricht an Bob mit dem Absendernamen Alice.

Bob und Alice dachten beide, sie haben direkt miteinander verschlüsselt kommuniziert. In Wirklichkeit konnte die Spionierenden aber alles mitlesen.

Im Internet können diese Spionierenden an jedem Router dieser Welt sein. Egal ob in deinem Router zuhause oder in einem großen Netzwerkknoten vor den großen Glasfaserkabeln in Richtung eines anderen Kontinents.

Die Lösung

Diese Authentizität, also die Echtheit einer Person, lässt sich mit Signaturen umsetzen.

Hash

Im ersten Schritt wird aus einer Nachricht ein Hash berechnet. Unter einem Hash kannst du dir eine Quersumme von einem Text vorstellen.

Beispiel Quersumme:

INPUT (Klartext):      caesar
Position im Alphabet:  3 1 5 19 1 18 
Berechnung Quersumme:  3 + 1 + 5 + 1 + 9 + 1 + 1 + 8
OUTPUT (Hashwert):     29

Eine Hashfunktion ist nur wesentlich komplizierter als eine einfache Quersumme, vom Prinzip her aber ähnlich.

Wichtig dabei ist:
1. Gibt man den gleichen Klartext hinein, so kommt immer der gleiche Hashwert am Ende raus.
2. Wird auch nur ein Buchstabe im Klartext geändert, so ändert sich der Hashwert komplett.
3. Aus dem Hash kann niemals der Klartext zurückgerechnet werden. Hashfunktionen sind kryptografische Einbahnstraßen.
4. Unterschiedliche Klartexte liefern niemals den gleichen Hashwert. (Kollisionen vermeiden)

Diese vier Regeln kannst du mit aktuellen Hashfunktionen einfach mal ausprobieren: https://hashgenerator.de/

Mit diesen Regeln können wir nun bestätigen, dass die Nachricht unverändert ist. Und zwar so:
Die Senderin einer Nachricht berechnet den Hashwert ihrer verfassten Nachricht. Der Empfänger dieser Nachricht errechnet ebenfalls den Hashwert der Nachricht, die bei ihm eingegangen ist. Unterscheiden sich die zwei Hashwerte, so wurde die Nachricht manipuliert. Sind sie identisch, so ist sie unverändert.

Eine Hashfunktion gilt als gebrochen, wenn ein zweiter Text gefunden wird, der den gleichen Hashwert hat wie ein anderer Text. Dadurch kann die eigentliche Nachricht ausgetauscht werden, der Hashwert bleibt gleich und der Empfänger denkt, die Nachricht ist nicht manipuliert worden.

So gilt z.B. der SHA-1 (Secure Hash Algorithm) seit 2005 als gebrochen und sollte nicht mehr verwendet werden. Sein Nachfolger ist SHA-2 (auch bekannt unter SHA-224, SHA-256, SHA-384, SHA-512), der zur Zeit als Standard definiert ist. Der Hauptunterschied ist seine erweiterte Bitlänge. Damit sind Kollisionen unwahrscheinlicher und aufwendiger zu berechnen. Eine komplett andere Hash-Konstruktion bietet dann erst SHA-3, welcher in der Praxis durch seine geringe Verbreitung noch nicht zum Einsatz kommt.

Signieren

Ist der Hashwert einer Nachricht berechnet, so wird dieser nun signiert. So kann verhindert werden, dass der Hashwert ebenfalls manipuliert wird und gleichzeitig wird eindeutig bestätigt, wer die Senderin der Nachricht war.

Dazu passiert fast das Gleiche, wie bei der RSA Verschlüsselung. Mit einem entscheidenden Unterschied. Die SENDERIN erstellt nun einen public key und einen private key. Nun verschlüsselt die Senderin den Hashwert ihrer Nachricht mit ihrem eigenen public key. Die Nachricht mit dem verschlüsselten Hashwert (Signatur) wird dem Empfänger zugesendet. Und jetzt passiert der große Unterschied zur RSA Verschlüsselung: Die Senderin veröffentlicht ihren private key!

Wie in einem Telefonbuch kann nun jede Person nachlesen welchen Key die Senderin hat. Der Empfänger der Nachricht kann nun also die Signatur mit dem öffentlichen Schlüssel der Senderin wieder entschlüsseln. Den dabei sichtbaren Hashwert der eigentlichen Nachricht kann er nun mit dem von ihm selbst errechneten Hashwert vergleichen. Ist dieser identisch, so kam die Nachricht eindeutig von der erwarteten Senderin und wurde nicht manipuliert.

Wichtig ist zu verstehen, dass die Nachricht selbst dabei gar nicht verschlüsselt sein muss. So kann auch eine für alle sichtbare Nachricht signiert werden und deren Verfasser eindeutig gemacht werden. Dies ist z.B. bei digitalen Verträgen wichtig, damit niemand der Parteien seine Unterschrift abstreiten kann.

Schlüsselverwaltung

Egal ob beim Signieren oder der asymmetrischen Verschlüsseln – die Schlüssel selbst müssen sicher zu den Personen gelangen, die sie benötigen. Diese Schlüsselverwaltung kannst du dir wie ein großes Telefonbuch vorstellen. In diesem Telefonbuch stehen die Namen von Personen und daneben der public key für z.B. die RSA Verschlüsselung und noch einmal daneben der private key der Signaturen dieser Person. (Die zwei keys müssen in jedem Fall separat generiert werden und dürfen niemals zusammenhängen)

Willst du nun eine Signatur einer Person prüfen, so kannst du einfach in diesem Telefonbuch nachschauen. Gleiches gilt für das Verfassen von Nachrichten und der Verschlüsselung mit dem public key des Empfängers.

Das Problem dieser Telefonbücher ist jedoch das Vertrauen. Wird dieses Telefonbuch zentral betrieben, dann musst du der Organisation vertrauen, die es zur Verfügung stellt. Ist die Organisation korrupt oder hat böswillige Absichten, dann kann ein Key ganz einfach ausgetauscht werden und somit ein man-in-the-middle Angriff durchgeführt werden.

Deshalb basiert in der Kryp­to­lgrafie alles auf Vertrauen und Misstrauen.

Beispiele aus dem Alltag

Sichere Webseiten – https

Hier gibt es eine dezentrale Schlüsselverwaltung. Das heißt, man hat sich im Internet darauf geeinigt, bestimmten Zertifizierungsstellen zu vertrauen. Diese dürfen Zertifikate für Webseiten ausstellen. Die Webseiten wiederum signieren mit diesem Zertifikat die Schlüssel ihrer https Verbindungen.

Öffnest du also die Seite https://farbenmeer.de, so sendet unser Server dir einen öffentlichen Schlüssel, mit dem du alle deine Daten verschlüsseln sollst, bevor du sie an den Server zurück sendest. Dieser öffentliche Schlüssel ist nun signiert, mit einem Schlüssel/Zertifikat der Zertifizierungsstelle. Und da dein Browser dieser Zertifizierungsstelle vertraut, vertraut er auch darauf, dass dieser öffentliche Schlüssel der farbenmeer Seite auch wirklich gehört und nicht von irgendjemandem ausgetauscht wurde.

Ist die Zertifizierungsstelle nun korrupt, so kann sie einfach Zertifikate auf farbenmeer.de ausstellen, auf Personen denen die Seite nicht gehört. Diese können sich dann sehr einfach als farbenmeer.de ausgeben und dir schädliche Inhalte wie z.B. Viren oder Trojaner unterjubeln.

Eine Zertifizierungsstelle hat deshalb klare Regeln, die sie beachten muss, damit ihr vertraut wird. Tut sie dies nicht, wird ihr auch mal kurzerhand das Vertrauen entzogen und alle Webseiten, die ein Zertifikat von dieser Stelle haben, gelten dann im Browser als unsicher und sind nicht mehr aufrufbar.

WhatsApp

Bei WhatsApp spricht man von einer Ende-zu-Ende Verschlüsselung mit zentraler Schlüsselverwaltung. Das heißt, die Inhalte sind von einem Ende, der Senderin, bis zum anderen Ende, dem Empfänger, durchgehend verschlüsselt. Niemand - auch nicht WhatsApp selbst - kann die Inhalte der Kommunikation lesen. Ein Angreifer muss somit auf dem Endgerät selbst aktiv werden, um zu erfahren, was in der Nachricht steht. Deshalb gibt es in Deutschland die Möglichkeit des Staatstrojaners. Also einem Trojaner, der von einer Polizeibehörde auf dem Endgerät platziert wird, um Daten (z.B. Chatinhalte) abzugreifen. Das nur nebenbei.

Die Schlüsselverwaltung läuft zentral über die Server von WhatsApp bzw. Facebook. Das oben genannte Telefonbuch liegt also zentral an einer Stelle. Nur Facebook hat die Macht hier Änderungen vorzunehmen. Will Facebook einen Schlüssel manipulieren oder wird per Gesetz dazu gezwungen, so würde dies nicht weiter auffallen und ein man in the middle Angriff wäre einfach durchzuführen.

Gehst du in der App auf einen Chat und dessen Einstellungen, so steht dort "Verschlüsselung". Tippe darauf. Nun siehst du einen QR-Code und den Fingerprint des shared secrets aus dem public key des Anderen. Ihr könnt hier nun den Code vergleichen, um sicherzustellen, dass WhatsApp eure Schlüssel nicht manipuliert hat.